はじめに

こんにちは、TechBulkです。 大学の「符号理論」の講義も第4回を迎えました。

これまでは、与えられた生成行列 $G$ や検査行列 $H$ を「絶対的なルール」として扱ってきましたが、今回は少し視点を変えて、「この行列 $G$ は、自分たちで使いやすいように作り変えてもいいのか？」 というテーマに踏み込みます。

結論から言うと、線形代数のルールに従っていれば、行列の形を変えても「符号としての本質（性能）」は変わりません。これを「同値な符号」と呼びます。

今回は、この性質を利用して、符号化・復号を劇的に簡単にする「組織符号」という形式を作り出すプロセスをまとめます。

以下のイメージ図は、この記事の内容に基づいてNano Banana Proに作ってもらいました。

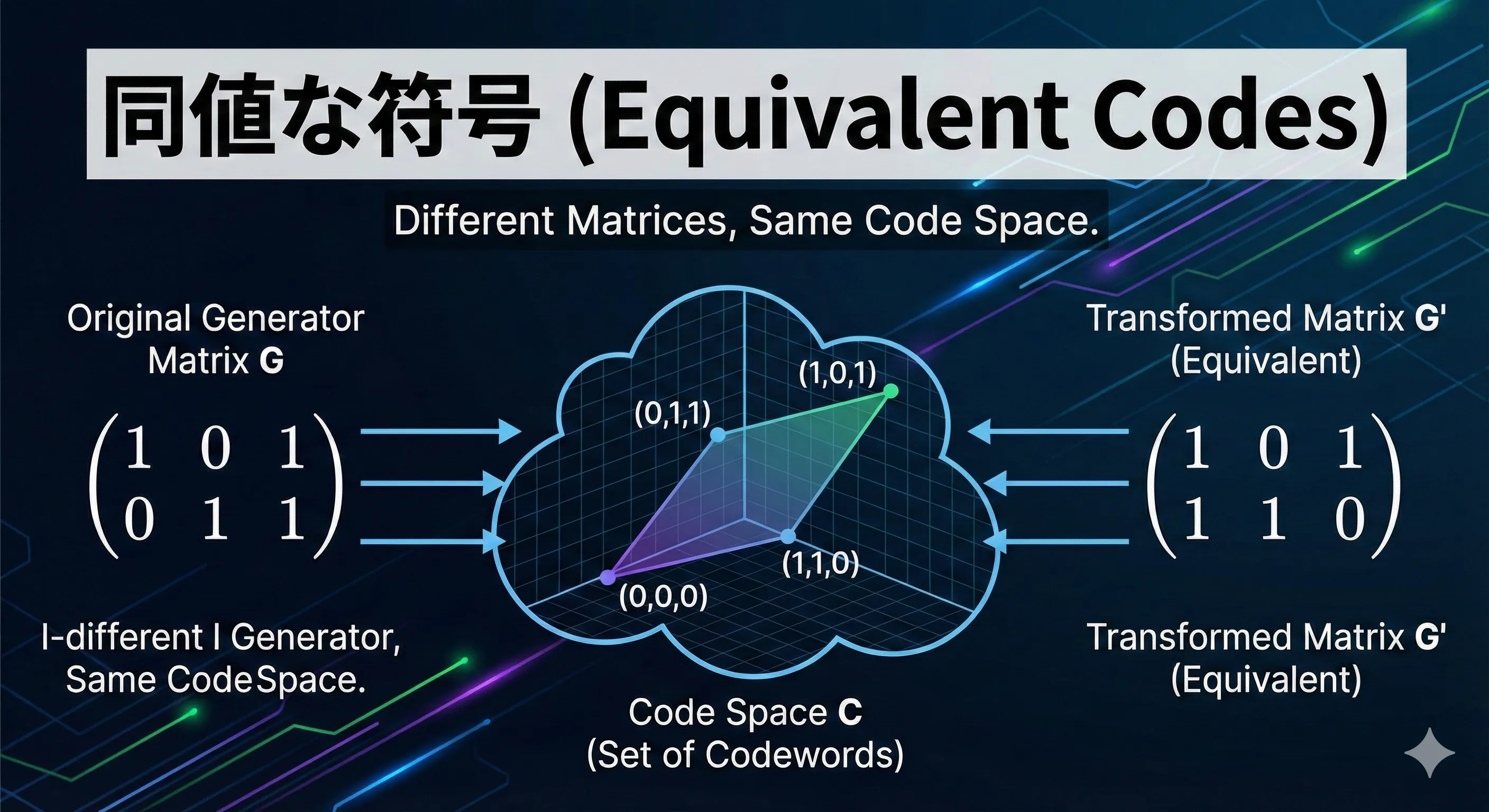
1. 生成行列 $G$ を変形してみる

生成行列 $G$ は、送りたいメッセージ $\boldsymbol{w}$ を、通信用の符号語 $\boldsymbol{x}$ に変換する「変換装置」のようなものです（式で書くと $\boldsymbol{x} = \boldsymbol{w}G$）。

ここで、線形代数で習った「行基本変形」を思い出してみましょう。特に符号理論（0と1の世界）で重要なのは、以下の操作です。

ある行に、別の行を足す

この操作を行列 $G$ に行っても良いのでしょうか？ 具体例で実験してみます。

実験：行列を変形すると何が起きる？

例えば、以下のようなシンプルな生成行列 $G$ があるとします。

$$G = \begin{pmatrix} 1 & 0 & 1 \\ 0 & 1 & 1 \end{pmatrix}$$

この行列を使って、2ビットのメッセージ（00, 01, 10, 11）を符号化すると、以下の4つの符号語が生まれます。 これが、この符号が持つ「正しいデータのリスト（集合）」です。

• 符号語の集合 $\mathcal{C}$ = { (0,0,0), (0,1,1), (1,0,1), (1,1,0) }

では、ここで $G$ の「2行目に1行目を足す」という変形をして、新しい行列 $G'$ を作ってみましょう。（※ $1+1=0$ に注意！）

$$G' = \begin{pmatrix} 1 & 0 & 1 \\ 1 & 1 & 0 \end{pmatrix} \leftarrow (2\text{行目} + 1\text{行目})$$

形が変わってしまったこの $G'$ を使って、もう一度符号化してみます。

メッセージ $\boldsymbol{w}$	(A) 元の $G$ で作った符号語	(B) 変形後 $G'$ で作った符号語
$[0, 0]$	$(0, 0, 0)$	$(0, 0, 0)$
$[0, 1]$	$(0, 1, 1)$	$(1, 1, 0)$
$[1, 0]$	$(1, 0, 1)$	$(1, 0, 1)$
$[1, 1]$	$(1, 1, 0)$	$(0, 1, 1)$

表を見ると、例えば「01」というメッセージが、(A)では「011」、(B)では「110」になり、対応関係は変わってしまいました。

しかし、(B)で作られた4つの符号語全体をよーく見てください。 $\{ (0,0,0), (1,1,0), (1,0,1), (0,1,1) \}$

順番は違いますが、「符号語のメンバー（集合）」は元の(A)と完全に一致しています。

これが「同値な符号」

このように、行列に行基本変形を行っても、生成される「符号語の空間」そのものは変化しません。 これを「同値な符号」と呼びます。

• 変わるもの: 「どのメッセージ」が「どの符号語」になるかという対応関係
• 変わらないもの: 符号語の集合そのもの、および符号の性能（誤り訂正能力）

2. 同値な符号が導く「組織符号」

中身が変わらないなら、人間やコンピュータにとって一番扱いやすい形に行列を変形してしまえばいいわけです。 そこで目指すゴールが「組織符号（Systematic Code）」です。

行基本変形や列の入れ替えを駆使して、生成行列 $G$ を以下のような標準形に変形します。

$$G' = [ I_k \mid P ]$$

• $I_k$ : 左側に $k \times k$ の単位行列（対角線が1で他が0の行列）を作る
• $P$ : 右側はそれ以外の余った部分

組織符号の何が嬉しいのか？

生成行列がこの形になると、符号化の結果が劇的に分かりやすくなります。 例えばメッセージ $\boldsymbol{w} = [w_1, w_2]$ を符号化すると…

$$\boldsymbol{x} = [w_1, w_2] \cdot [ I \mid P ] = [\underbrace{w_1, w_2}_{\text{メッセージそのまま}} \mid \underbrace{p_1, p_2}_{\text{検査ビット}}]$$

このように、「符号語の前半を見れば、元のメッセージがそのまま書いてある」という状態になります。 これなら、受信側はパリティチェックさえ通れば、復号計算をしなくても先頭を見るだけでデータを読めます。これが組織符号の最大のメリットです。

3. 生成行列 $G$ から検査行列 $H$ を一瞬で作る方法

今回の講義で一番の実践テクニックがこれです。 生成行列を組織符号の形 $G = [ I_k \mid P ]$ にさえ変形できれば、対になるパリティ検査行列 $H$ は、計算なしで自動的に決まります。

$$H = [ P^T \mid I_{n-k} ]$$

• $P^T$ : 行列 $P$ の転置行列（行と列を入れ替えたもの）
• $I_{n-k}$ : 右側に単位行列をくっつける

なぜこれでいいの？（直交性の確認）

本当にこの $H$ でいいのか、確かめてみましょう。 正しい符号語を作る $G$ と、検査する $H$ は、直交（積がゼロ行列）する必要があります。

$$\begin{aligned} G H^T &= [ I \mid P ] \cdot [ P^T \mid I ]^T \\ &= [ I \mid P ] \cdot \begin{pmatrix} P \\ I \end{pmatrix} \\ &= I \cdot P + P \cdot I \\ &= P + P \end{aligned}$$

デジタルの世界（GF(2)）では、$1+1=0$ なので、同じ行列を足すと必ずゼロ行列（$O$）になります。 つまり、$GH^T = O$ が成立し、これが正しい検査行列であることが証明されました。

「$G$ を掃き出し法で $[I \mid P]$ にして、右側の $P$ を転置して単位行列を添えれば $H$ の完成」 この手順は、テストや今後の設計で頻繁に使うことになりそうです。

4. 性能（誤り訂正能力）は変わらない

最後に、重要なポイントを確認しておきます。 「行列を勝手に変形して、誤り訂正能力は落ちないの？」という疑問です。

結論は、「全く落ちない（変わらない）」です。

前回の記事で触れた通り、符号の性能（最小距離 $d_{min}$）は、「符号語の集合の中で、最も重みが小さい（1が少ない）ものの数」で決まります。 同値な符号への変形では、符号語の集合（メンバー）そのものは1つも変わっていないので、当然その中の最小重みも変わりません。

つまり、安心して計算しやすい形（組織符号）に変形して運用して良いということです。

まとめ

今回の講義の要点は以下の3つです。

1. 同値な符号: 生成行列 $G$ に行基本変形を行っても、作られる符号語の空間（セット）は変わらない。
2. 組織符号: この性質を使って $G = [I \mid P]$ という形に変形すると、メッセージがそのまま見えるので非常に便利。
3. $H$ の導出: 組織符号形式にすれば、$H = [P^T \mid I]$ として検査行列を即座に作れる。

線形代数の「行列変形」が、ただの計算練習ではなく、「システムを使いやすく最適化する手段」として使われているのが面白い点でした。 次回は、いよいよ具体的な符号の構成法や、より高度な代数の話に進んでいきそうです。