はじめに

こんにちは、TechBulkです。 前回の記事では、行列を変形しても符号の性質が変わらない「同値な符号」について学びました。

今回は、いよいよハミング符号の進化版である「拡大ハミング符号（Extended Hamming Code）」について解説します。

通常の(7,4,3)ハミング符号は「1ビットの誤り」を訂正できました。しかし、「2ビットの誤り」が起きると、間違った訂正をしてしまうという弱点がありました。 そこで登場するのが、全体の長さを1ビットだけ増やした(8,4,4)拡大ハミング符号です。

たった1ビット増やすだけで、なぜ性能が向上するのか？ その数学的な仕組みと、パリティ検査行列 $H$ の見事な拡張方法についてまとめます。

以下のイメージ図は、この記事の内容に基づいてNano Banana Proに作ってもらいました。

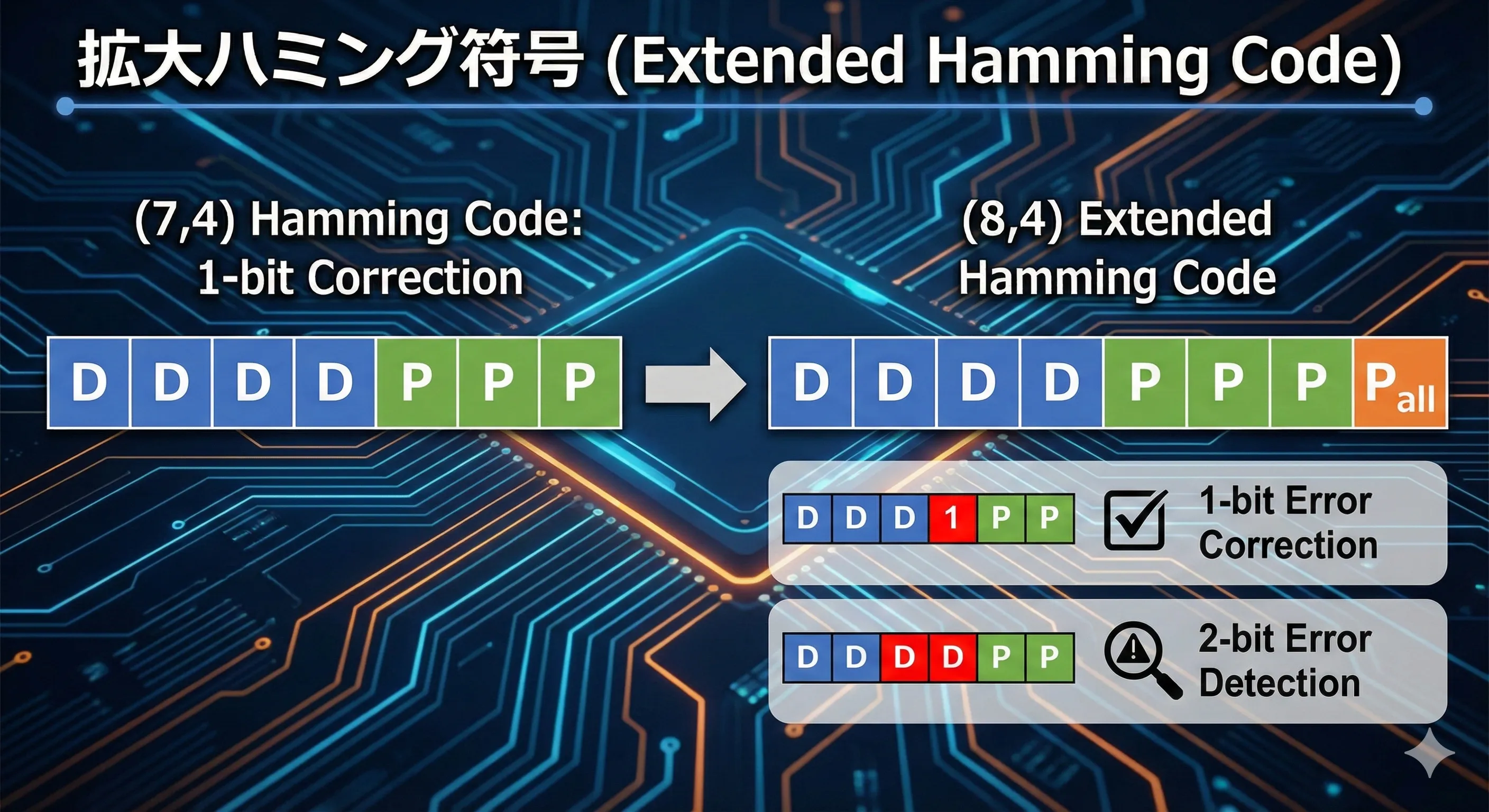
1. パリティ検査行列 $H$ の拡張プロセス

まずは、どのようにして通常のハミング符号から拡大ハミング符号を作るのか、その「行列の拡張」の手順を見ていきます。

ベースとなる(7,4,3)ハミング符号

元となる(7,4,3)ハミング符号のパリティ検査行列 $H$（3行7列）を用意します。これを $H_{org}$ とします。

$$H_{org} = \begin{pmatrix} 1 & 1 & 1 & 0 & 1 & 0 & 0 \\ 0 & 1 & 1 & 1 & 0 & 1 & 0 \\ 1 & 1 & 0 & 1 & 0 & 0 & 1 \end{pmatrix}$$

拡張のアイデア：偶数パリティの追加

この符号に、さらに1ビットの「全ビットの偶数パリティ」（符号語に含まれる1の個数が偶数になるようにするビット）を追加します。 長さは7から8に伸びます。

これを実現するために、行列 $H$ を以下のように拡張します。

1. 新しい行の追加: 符号語 $\boldsymbol{x} = (x_1, \dots, x_8)$ の成分をすべて足すと0になる（偶数個の1が含まれる）という条件を追加します。

   $$x_1 + x_2 + \dots + x_8 = 0 \pmod 2$$

   これを式で表すと、成分がすべて1の行ベクトル $\boldsymbol{r}_4 = [1, 1, \dots, 1]$ を $H$ の最下段に追加することになります。

2. 新しい列の追加: 8ビット目を表すための新しい列を追加します。 ここで、元の $H_{org}$ の各行（1〜3行目）に対して、新しく追加する8ビット目 $x_8$ が影響を与えないようにする必要があります。 そのため、新しい列の1〜3行目はすべて 0 に設定します。

完成した拡大ハミング符号の行列 $H'$

以上の操作を合わせると、(8,4,4)拡大ハミング符号の検査行列 $H'$ は以下のようになります（4行8列）。

$$H' = \begin{pmatrix} & & & & & & & \mathbf{0} \\ & & H_{org} & & & & & \mathbf{0} \\ & & & & & & & \mathbf{0} \\ \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} \end{pmatrix}$$

具体的に数字を入れるとこうなります。

$$H' = \begin{pmatrix} 1 & 1 & 1 & 0 & 1 & 0 & 0 & \mathbf{0} \\ 0 & 1 & 1 & 1 & 0 & 1 & 0 & \mathbf{0} \\ 1 & 1 & 0 & 1 & 0 & 0 & 1 & \mathbf{0} \\ \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} & \mathbf{1} \end{pmatrix}$$

この行列 $H'$ の特徴は、「全ての列ベクトルの最下段（4行目）が必ず 1 になっている」という点です。これが後の誤り検出で非常に重要になります。

2. 1ビット誤りは訂正できるのか？（確認）

では、この新しい行列 $H'$ を使って、従来通り1ビットの誤りが訂正できるか確認してみます。

受信データに1ビットの誤り $e_i$ （$i$ 番目のビットだけが1のベクトル）が乗ったとします。 シンドローム $s$ を計算すると、以下のようになります。

$$s = H' e_i^T = h_i$$

ここで $h_i$ は行列 $H'$ の $i$ 番目の列ベクトルです。 拡大ハミング符号の行列 $H'$ を見ると、すべての列ベクトル $h_i$ は互いに異なります。

• $h_1 = (1,0,1,1)^T$
• $h_2 = (1,1,1,1)^T$
• …

計算されたシンドローム $s$ がどの列 $h_i$ と一致するかを見れば、誤り位置 $i$ を特定できます。つまり、1ビット誤りは問題なく訂正可能です。

3. なぜ「2ビット誤り」を検出できるのか？

ここからが本題です。通常のハミング符号ではお手上げだった「2ビット誤り」を、拡大ハミング符号はどうやって見分けるのでしょうか。

2ビット誤りのシンドローム

2箇所のビット（$i$番目と$j$番目）が反転した誤りを考えます。誤りベクトルは $e = e_i + e_j$ となります。 この時のシンドローム $s$ は次のようになります。

$$s = H' (e_i + e_j)^T = H'e_i^T + H'e_j^T = h_i + h_j$$

つまり、「2つの列ベクトルの和」になります。

「最下段の1」が生み出す違い

ここで、先ほど確認した $H'$ の構造が効いてきます。 $H'$ の全ての列ベクトル $h_k$ の 最下段（4行目）は必ず 1 でした。

では、シンドローム $s$ の最下段（4行目の成分）に注目して、1ビット誤りと2ビット誤りを比較してみましょう。

• 1ビット誤りの場合 ($s = h_i$): 最下段は $1$ です。
• 2ビット誤りの場合 ($s = h_i + h_j$): 最下段は $1 + 1 = 0 \pmod 2$ となり、必ず 0 になります。

判定アルゴリズム

この性質を利用すると、受信側は以下のように振る舞うことができます。

1. シンドローム $s$ を計算する。
2. もし $s = \mathbf{0}$ なら、誤りなし。
3. もし $s \neq \mathbf{0}$ の場合：
   • $s$ の最下段が 1 なら $\rightarrow$ 「1ビット誤り」と判断し、訂正を行う。
   • $s$ の最下段が 0 なら $\rightarrow$ 「2ビット（以上の偶数個の）誤り」と判断し、訂正はせずに「誤り検出」を報告する。

2ビット誤りのシンドローム $h_i + h_j$ は、どの1ビット誤りのシンドローム $h_k$ とも一致しません（最下段が0と1で違うため）。 これにより、誤訂正することなく、「あ、これは2ビット間違っているから直せないな」と気づくことができるのです。

4. 最小距離 $d_{min}=4$ の意味

最後に、距離の観点から整理します。 この拡大ハミング符号の最小ハミング距離は $d_{min} = 4$ です。

• 1ビット訂正: 距離3が必要（半径1の球が重ならない）
• 2ビット検出: 距離3があれば可能（1ビット誤りと区別がつかないが、0ではないと分かる）

距離が4に伸びたことで、 「符号語」から1歩離れた「1ビット誤り」と、2歩離れた「2ビット誤り」が、空間上で明確に区別されるようになりました。

• 距離1の点 $\rightarrow$ 1ビット誤りとして訂正（最も近い符号語へ戻す）
• 距離2の点 $\rightarrow$ 2ビット誤りとして検出（どっちの符号語からも等距離なので戻せないが、誤りであることは確定）

まとめ

今回の講義のポイントは以下の通りです。

1. 拡張: ハミング符号に「全体のパリティビット」を1つ加えることで拡大ハミング符号を作る。
2. 行列: 検査行列 $H'$ の最下段はすべて1になる。
3. 判定: シンドロームの最下段が1なら「訂正可能（1ビット誤り）」、0なら「検出のみ（2ビット誤り）」と見分けることができる。

たった1行1列を付け足すだけで、システムの信頼性が大きく向上する。線形代数の性質を巧みに利用した、非常に美しい設計だと感じました。

次回は、いよいよ巡回符号や多項式表現などのより高度な符号化技術に進んでいく予定です。