はじめに

こんにちは、TechBulkです。

前回の記事（vol.8）では、「原始既約多項式」の根 $\alpha$ を添加することで、計算しやすい拡大体 $GF(2^m)$ が作れるという話をしました。

しかし、ここで一つの疑問が湧きます。

「既約多項式（因数分解できない多項式）なら、なんでもいいんじゃないの？」 「わざわざ『原始』 とついているのはなぜ？」

実は、すべての「既約多項式」が「原始多項式」であるわけではありません。 今回は、この少しややこしい定義の違いと、「原始多項式でなければならない理由」について深掘りします。

1. 定義の整理：既約と原始

まずは、2つの言葉の定義を明確にしましょう。

① 既約多項式（Irreducible Polynomial）

これは「多項式の世界における素数」です。 これ以上低い次数の多項式の積に因数分解できない多項式のことです。

• 条件: $f(x)$ が $g(x)h(x)$ の形に分解できない。
• 役割: これを法（mod）とすることで、割り算ができる「体（Field）」を作ることができます。

② 原始多項式（Primitive Polynomial）

これは「巡回群の生成元（原始元）を根に持つ多項式」です。 既約多項式の中でも、特にエリートな性質を持つものです。

• 条件: $m$ 次の多項式 $f(x)$ の根 $\alpha$ の位数が $2^m - 1$ であること。
  • つまり、$\alpha^1, \alpha^2, \dots$ と計算していったとき、$2^m-1$ 乗して初めて $1$ に戻る（途中で $1$ にならない）こと。
• 役割: これを使うと、体の要素（$0$以外）を $\alpha$ のべき乗ですべて表現できる（巡回群になる）。

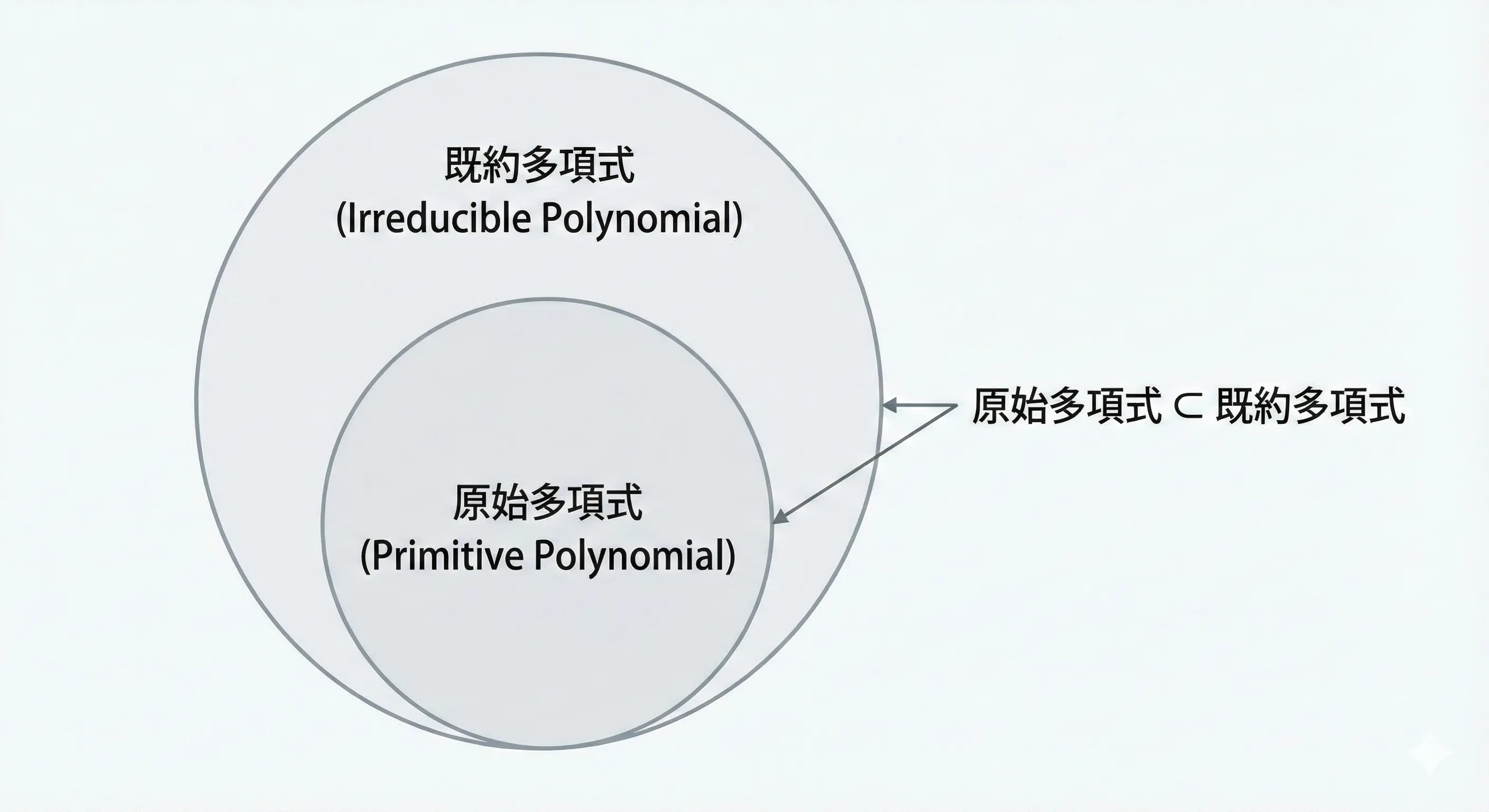
関係性としては、以下のようになります。 原始多項式 $\subset$ 既約多項式 （原始多項式は、必ず既約多項式です。しかし、既約多項式が必ずしも原始多項式とは限りません。）

2. 「既約だけど原始じゃない」例

この違いを理解するには、反例を見るのが一番早いです。 $GF(2)$ 上の 4次 の世界で考えてみましょう。

4次の拡大体 $GF(2^4) = GF(16)$ を作るには、4次の既約多項式が必要です。 実は、4次の既約多項式は以下の3つしかありません。

1. $x^4 + x + 1$
2. $x^4 + x^3 + 1$
3. $x^4 + x^3 + x^2 + x + 1$

上2つは「原始既約多項式」ですが、3つ目の $h(x) = x^4 + x^3 + x^2 + x + 1$ は、既約ですが原始多項式ではありません。

実験：なぜダメなのか？

この $h(x)$ の根を $\beta$ としましょう。つまり、$h(\beta) = 0$ です。 この $\beta$ をどんどん掛け算（べき乗）して、いつ $1$ になるか（周期）を調べてみます。 期待する周期は、$GF(16)$ の0以外の要素数なので、$16 - 1 = 15$ です。

しかし…

$$\begin{aligned} \beta^1 &= \beta \\ \beta^2 &= \beta^2 \\ \beta^3 &= \beta^3 \\ \beta^4 &= \beta^3 + \beta^2 + \beta + 1 \quad (\because \beta^4 + \beta^3 + \beta^2 + \beta + 1 = 0) \\ \beta^5 &= \beta(\beta^3 + \beta^2 + \beta + 1) \\ &= \beta^4 + \beta^3 + \beta^2 + \beta \\ &= (\beta^3 + \beta^2 + \beta + 1) + \beta^3 + \beta^2 + \beta \\ &= 1 \quad (\text{同じものを足すと消えるので}) \end{aligned}$$

なんと、たった5回掛けただけで $1$ に戻ってしまいました。

$$\beta^5 = 1$$

これでは、$\{ \beta^0, \beta^1, \beta^2, \beta^3, \beta^4 \}$ の 5個の要素 しか表現できません。 $GF(16)$ には $0$ を除いて15個の要素があるはずなのに、これでは全然足りませんね。

つまり、この多項式で作った体は「体」としては成立していますが、その根 $\beta$ は「原始元」ではないため、便利な「べき乗表現」ですべての要素を表すことができないのです。

3. なぜ符号理論で「原始」が好まれるのか？

符号理論、特にリード・ソロモン符号やBCH符号などの実装では、計算速度が命です。

• 原始多項式を使う場合:
  • すべての要素を $\alpha^i$ で表せる。
  • 掛け算は指数の足し算（$i+j \pmod{2^m-1}$）だけで終わる。超高速！
• 原始多項式じゃない場合:
  • すべての要素を1つの元のべき乗で表せない。
  • 掛け算をするたびに多項式の剰余計算が必要になる。遅いし面倒！

だからこそ、私たちは教科書で「原始既約多項式」を選んで使っているのです。

4. 今回のまとめ

ちなみに、コンピュータで計算する際は、有名な原始多項式のリスト（テーブル）を参照して使うのが一般的です。 次回はいよいよ、これらの知識を使って実際にデータを符号化する「BCH符号」や「リード・ソロモン符号」の入り口に立ってみましょう。